Nice puzzle
bob and sue are implied in the question but heres a little more detail
bob takes his first throw and has a 5 in 6 chance of not hitting a 6
sue takes her first throw and has a 5 in 6 chance of not hitting a 6
bob takes his second throw and has a 1 in 6 chance of hitting a 6
so the odds that bob will throw a 6 on his 2nd throw are
(5/6) * (5/6) * (1/6)
maybe thats wrong ? but it seems right to me
bob takes his first throw and has a 5 in 6 chance of not hitting a 6
sue takes her first throw and has a 5 in 6 chance of not hitting a 6
bob takes his second throw and has a 1 in 6 chance of hitting a 6
so the odds that bob will throw a 6 on his 2nd throw are
(5/6) * (5/6) * (1/6)
maybe thats wrong ? but it seems right to me
Writing code is easy. Finishing is hard.
Then just leave them outrumpole wrote:bob and sue are implied in the question but heres a little more detail
Correct, but it's not the question that was asked.rumpole wrote:so the odds that bob will throw a 6 on his 2nd throw are
(5/6) * (5/6) * (1/6)
maybe thats wrong ? but it seems right to me
- Jonathan
- A Brave Victim
- Posts: 3391
- Joined: Thu Feb 03, 2005 12:50 am
- Location: Not really lurking anymore
rumpole, "Bob rolls a 6 before Sue." isn't meant to be ignored, nor is "What is the probability Bob rolled the 6 on his second turn?"
---
I got bored and recorded a few (ahem) actual dice rolls, and made a program to automate interpretation and all that.
Dice specs: wooden, painted red, shaped like the intersection of a sphere and a cube (so that the cube's edges are engulfed, but just barely), not heavy enough to influence results by hitting the keyboard.
---
I got bored and recorded a few (ahem) actual dice rolls, and made a program to automate interpretation and all that.
Dice specs: wooden, painted red, shaped like the intersection of a sphere and a cube (so that the cube's edges are engulfed, but just barely), not heavy enough to influence results by hitting the keyboard.
Pretty close to expected (by some of us).Scroll down to see final stats wrote:6 | Sue1 | Win
2 | Sue1
2 | Bob1
6 | Sue2 | Win
5 | Sue1
6 | Bob1 | Win | Recording Bob: 1 | Bob2/Bob = 0/1 = 0
2 | Sue1
1 | Bob1
3 | Sue2
5 | Bob2
5 | Sue3
1 | Bob3
1 | Sue4
1 | Bob4
6 | Sue5 | Win
2 | Sue1
1 | Bob1
1 | Sue2
1 | Bob2
1 | Sue3
6 | Bob3 | Win | Recording Bob: 2 | Bob2/Bob = 0/2 = 0/1 = 0
1 | Sue1
3 | Bob1
6 | Sue2 | Win
6 | Sue1 | Win
4 | Sue1
3 | Bob1
3 | Sue2
1 | Bob2
2 | Sue3
2 | Bob3
3 | Sue4
5 | Bob4
5 | Sue5
6 | Bob5 | Win | Recording Bob: 3 | Bob2/Bob = 0/3 = 0/1 = 0
1 | Sue1
3 | Bob1
4 | Sue2
6 | Bob2 | Win | Recording Bob: 4 | Recording Bob2: 1 | Bob2/Bob = 1/4 = 0.25
3 | Sue1
2 | Bob1
3 | Sue2
4 | Bob2
6 | Sue3 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 5 | Bob2/Bob = 1/5 = 0.2
2 | Sue1
1 | Bob1
6 | Sue2 | Win
5 | Sue1
1 | Bob1
2 | Sue2
3 | Bob2
1 | Sue3
4 | Bob3
2 | Sue4
5 | Bob4
3 | Sue5
3 | Bob5
5 | Sue6
6 | Bob6 | Win | Recording Bob: 6 | Bob2/Bob = 1/6 = 0.1(6)
6 | Sue1 | Win
6 | Sue1 | Win
6 | Sue1 | Win
3 | Sue1
6 | Bob1 | Win | Recording Bob: 7 | Bob2/Bob = 1/7 = 0.(142857)
3 | Sue1
4 | Bob1
1 | Sue2
2 | Bob2
2 | Sue3
2 | Bob3
4 | Sue4
4 | Bob4
1 | Sue5
3 | Bob5
6 | Sue6 | Win
3 | Sue1
3 | Bob1
5 | Sue2
3 | Bob2
4 | Sue3
5 | Bob3
1 | Sue4
5 | Bob4
4 | Sue5
1 | Bob5
4 | Sue6
2 | Bob6
2 | Sue7
5 | Bob7
4 | Sue8
3 | Bob8
4 | Sue9
3 | Bob9
4 | Sue10
6 | Bob10 | Win | Recording Bob: 8 | Bob2/Bob = 1/8 = 0.125
2 | Sue1
4 | Bob1
4 | Sue2
2 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 9 | Bob2/Bob = 1/9 = 0.(1)
5 | Sue1
3 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 10 | Recording Bob2: 2 | Bob2/Bob = 2/10 = 1/5 = 0.2
1 | Sue1
4 | Bob1
2 | Sue2
4 | Bob2
5 | Sue3
2 | Bob3
1 | Sue4
4 | Bob4
6 | Sue5 | Win
4 | Sue1
1 | Bob1
5 | Sue2
2 | Bob2
3 | Sue3
2 | Bob3
6 | Sue4 | Win
6 | Sue1 | Win
2 | Sue1
4 | Bob1
5 | Sue2
1 | Bob2
6 | Sue3 | Win
2 | Sue1
4 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 11 | Recording Bob2: 3 | Bob2/Bob = 3/11 = 0.(27)
3 | Sue1
3 | Bob1
6 | Sue2 | Win
6 | Sue1 | Win
6 | Sue1 | Win
6 | Sue1 | Win
2 | Sue1
1 | Bob1
3 | Sue2
4 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 12 | Bob2/Bob = 3/12 = 1/4 = 0.25
6 | Sue1 | Win
6 | Sue1 | Win
4 | Sue1
1 | Bob1
4 | Sue2
4 | Bob2
4 | Sue3
3 | Bob3
2 | Sue4
4 | Bob4
6 | Sue5 | Win
5 | Sue1
5 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 13 | Recording Bob2: 4 | Bob2/Bob = 4/13 = 0.(307692)
2 | Sue1
1 | Bob1
1 | Sue2
2 | Bob2
5 | Sue3
5 | Bob3
1 | Sue4
4 | Bob4
6 | Sue5 | Win
4 | Sue1
1 | Bob1
2 | Sue2
4 | Bob2
1 | Sue3
2 | Bob3
4 | Sue4
5 | Bob4
3 | Sue5
1 | Bob5
3 | Sue6
1 | Bob6
5 | Sue7
6 | Bob7 | Win | Recording Bob: 14 | Bob2/Bob = 4/14 = 2/7 = 0.(285714)
2 | Sue1
4 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 15 | Recording Bob2: 5 | Bob2/Bob = 5/15 = 1/3 = 0.(3)
2 | Sue1
5 | Bob1
4 | Sue2
6 | Bob2 | Win | Recording Bob: 16 | Recording Bob2: 6 | Bob2/Bob = 6/16 = 3/8 = 0.375
4 | Sue1
6 | Bob1 | Win | Recording Bob: 17 | Bob2/Bob = 6/17 = 0.(3529411764705882)
2 | Sue1
3 | Bob1
2 | Sue2
1 | Bob2
5 | Sue3
4 | Bob3
5 | Sue4
3 | Bob4
3 | Sue5
5 | Bob5
6 | Sue6 | Win
4 | Sue1
3 | Bob1
6 | Sue2 | Win
6 | Sue1 | Win
2 | Sue1
4 | Bob1
6 | Sue2 | Win
3 | Sue1
1 | Bob1
1 | Sue2
1 | Bob2
5 | Sue3
1 | Bob3
2 | Sue4
1 | Bob4
5 | Sue5
5 | Bob5
5 | Sue6
6 | Bob6 | Win | Recording Bob: 18 | Bob2/Bob = 6/18 = 1/3 = 0.(3)
1 | Sue1
5 | Bob1
6 | Sue2 | Win
6 | Sue1 | Win
5 | Sue1
2 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 19 | Recording Bob2: 7 | Bob2/Bob = 7/19 = 0.(368421052631578947)
4 | Sue1
4 | Bob1
1 | Sue2
5 | Bob2
4 | Sue3
5 | Bob3
1 | Sue4
3 | Bob4
3 | Sue5
1 | Bob5
1 | Sue6
3 | Bob6
1 | Sue7
3 | Bob7
6 | Sue8 | Win
5 | Sue1
1 | Bob1
3 | Sue2
3 | Bob2
4 | Sue3
3 | Bob3
6 | Sue4 | Win
1 | Sue1
5 | Bob1
6 | Sue2 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 20 | Bob2/Bob = 7/20 = 0.35
1 | Sue1
4 | Bob1
4 | Sue2
5 | Bob2
5 | Sue3
5 | Bob3
5 | Sue4
6 | Bob4 | Win | Recording Bob: 21 | Bob2/Bob = 7/21 = 1/3 = 0.(3)
6 | Sue1 | Win
1 | Sue1
2 | Bob1
2 | Sue2
4 | Bob2
5 | Sue3
6 | Bob3 | Win | Recording Bob: 22 | Bob2/Bob = 7/22 = 0.3(18)
2 | Sue1
4 | Bob1
6 | Sue2 | Win
3 | Sue1
1 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 23 | Recording Bob2: 8 | Bob2/Bob = 8/23 = 0.(3478260869565217391304)
4 | Sue1
4 | Bob1
4 | Sue2
3 | Bob2
2 | Sue3
5 | Bob3
2 | Sue4
3 | Bob4
6 | Sue5 | Win
3 | Sue1
1 | Bob1
6 | Sue2 | Win
3 | Sue1
2 | Bob1
1 | Sue2
4 | Bob2
5 | Sue3
5 | Bob3
6 | Sue4 | Win
5 | Sue1
5 | Bob1
1 | Sue2
5 | Bob2
4 | Sue3
1 | Bob3
1 | Sue4
4 | Bob4
1 | Sue5
3 | Bob5
1 | Sue6
3 | Bob6
1 | Sue7
2 | Bob7
3 | Sue8
2 | Bob8
1 | Sue9
4 | Bob9
6 | Sue10 | Win
3 | Sue1
4 | Bob1
1 | Sue2
4 | Bob2
1 | Sue3
1 | Bob3
6 | Sue4 | Win
3 | Sue1
2 | Bob1
6 | Sue2 | Win
5 | Sue1
2 | Bob1
2 | Sue2
6 | Bob2 | Win | Recording Bob: 24 | Recording Bob2: 9 | Bob2/Bob = 9/24 = 3/8 = 0.375
6 | Sue1 | Win
3 | Sue1
1 | Bob1
6 | Sue2 | Win
2 | Sue1
5 | Bob1
6 | Sue2 | Win
3 | Sue1
3 | Bob1
5 | Sue2
2 | Bob2
6 | Sue3 | Win
2 | Sue1
6 | Bob1 | Win | Recording Bob: 25 | Bob2/Bob = 9/25 = 0.36
2 | Sue1
1 | Bob1
4 | Sue2
5 | Bob2
3 | Sue3
6 | Bob3 | Win | Recording Bob: 26 | Bob2/Bob = 9/26 = 0.3(461538)
1 | Sue1
4 | Bob1
6 | Sue2 | Win
5 | Sue1
6 | Bob1 | Win | Recording Bob: 27 | Bob2/Bob = 9/27 = 1/3 = 0.(3)
2 | Sue1
6 | Bob1 | Win | Recording Bob: 28 | Bob2/Bob = 9/28 = 0.32(142857)
6 | Sue1 | Win
2 | Sue1
2 | Bob1
5 | Sue2
5 | Bob2
5 | Sue3
4 | Bob3
2 | Sue4
6 | Bob4 | Win | Recording Bob: 29 | Bob2/Bob = 9/29 = 0.(3103448275862068965517241379)
4 | Sue1
5 | Bob1
3 | Sue2
4 | Bob2
2 | Sue3
6 | Bob3 | Win | Recording Bob: 30 | Bob2/Bob = 9/30 = 3/10 = 0.3
3 | Sue1
1 | Bob1
1 | Sue2
6 | Bob2 | Win | Recording Bob: 31 | Recording Bob2: 10 | Bob2/Bob = 10/31 = 0.(322580645161290)
6 | Sue1 | Win
6 | Sue1 | Win
6 | Sue1 | Win
6 | Sue1 | Win
3 | Sue1
5 | Bob1
1 | Sue2
3 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 32 | Bob2/Bob = 10/32 = 5/16 = 0.3125
5 | Sue1
5 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 33 | Recording Bob2: 11 | Bob2/Bob = 11/33 = 1/3 = 0.(3)
1 | Sue1
2 | Bob1
5 | Sue2
1 | Bob2
2 | Sue3
3 | Bob3
1 | Sue4
3 | Bob4
3 | Sue5
2 | Bob5
1 | Sue6
5 | Bob6
5 | Sue7
5 | Bob7
5 | Sue8
4 | Bob8
5 | Sue9
6 | Bob9 | Win | Recording Bob: 34 | Bob2/Bob = 11/34 = 0.3(2352941176470588)
1 | Sue1
1 | Bob1
2 | Sue2
1 | Bob2
4 | Sue3
4 | Bob3
4 | Sue4
1 | Bob4
2 | Sue5
6 | Bob5 | Win | Recording Bob: 35 | Bob2/Bob = 11/35 = 0.3(142857)
5 | Sue1
3 | Bob1
1 | Sue2
2 | Bob2
2 | Sue3
4 | Bob3
6 | Sue4 | Win
2 | Sue1
2 | Bob1
5 | Sue2
2 | Bob2
1 | Sue3
1 | Bob3
2 | Sue4
6 | Bob4 | Win | Recording Bob: 36 | Bob2/Bob = 11/36 = 0.30(5)
1 | Sue1
5 | Bob1
2 | Sue2
4 | Bob2
1 | Sue3
1 | Bob3
6 | Sue4 | Win
3 | Sue1
1 | Bob1
6 | Sue2 | Win
2 | Sue1
6 | Bob1 | Win | Recording Bob: 37 | Bob2/Bob = 11/37 = 0.(297)
1 | Sue1
2 | Bob1
2 | Sue2
5 | Bob2
4 | Sue3
1 | Bob3
6 | Sue4 | Win
3 | Sue1
6 | Bob1 | Win | Recording Bob: 38 | Bob2/Bob = 11/38 = 0.2(894736842105263157)
5 | Sue1
6 | Bob1 | Win | Recording Bob: 39 | Bob2/Bob = 11/39 = 0.(282051)
4 | Sue1
5 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 40 | Recording Bob2: 12 | Bob2/Bob = 12/40 = 3/10 = 0.3
5 | Sue1
3 | Bob1
1 | Sue2
2 | Bob2
4 | Sue3
2 | Bob3
1 | Sue4
4 | Bob4
1 | Sue5
2 | Bob5
4 | Sue6
6 | Bob6 | Win | Recording Bob: 41 | Bob2/Bob = 12/41 = 0.(29268)
5 | Sue1
5 | Bob1
5 | Sue2
2 | Bob2
5 | Sue3
5 | Bob3
6 | Sue4 | Win
6 | Sue1 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 42 | Bob2/Bob = 12/42 = 2/7 = 0.(285714)
6 | Sue1 | Win
6 | Sue1 | Win
4 | Sue1
1 | Bob1
2 | Sue2
3 | Bob2
2 | Sue3
5 | Bob3
3 | Sue4
5 | Bob4
5 | Sue5
4 | Bob5
4 | Sue6
2 | Bob6
1 | Sue7
2 | Bob7
4 | Sue8
6 | Bob8 | Win | Recording Bob: 43 | Bob2/Bob = 12/43 = 0.(279069767441860465116)
5 | Sue1
2 | Bob1
1 | Sue2
6 | Bob2 | Win | Recording Bob: 44 | Recording Bob2: 13 | Bob2/Bob = 13/44 = 0.29(54)
5 | Sue1
1 | Bob1
6 | Sue2 | Win
3 | Sue1
4 | Bob1
2 | Sue2
4 | Bob2
4 | Sue3
1 | Bob3
2 | Sue4
1 | Bob4
1 | Sue5
1 | Bob5
4 | Sue6
1 | Bob6
5 | Sue7
3 | Bob7
1 | Sue8
5 | Bob8
3 | Sue9
4 | Bob9
5 | Sue10
5 | Bob10
2 | Sue11
6 | Bob11 | Win | Recording Bob: 45 | Bob2/Bob = 13/45 = 0.2(8)
5 | Sue1
5 | Bob1
4 | Sue2
3 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 46 | Bob2/Bob = 13/46 = 0.2(8260869565217391304347)
3 | Sue1
3 | Bob1
3 | Sue2
2 | Bob2
5 | Sue3
6 | Bob3 | Win | Recording Bob: 47 | Bob2/Bob = 13/47 = 0.(2765957446808510638297872340425531914893617021)
6 | Sue1 | Win
4 | Sue1
3 | Bob1
3 | Sue2
1 | Bob2
2 | Sue3
1 | Bob3
1 | Sue4
3 | Bob4
5 | Sue5
4 | Bob5
6 | Sue6 | Win
4 | Sue1
1 | Bob1
1 | Sue2
5 | Bob2
5 | Sue3
2 | Bob3
4 | Sue4
4 | Bob4
5 | Sue5
4 | Bob5
2 | Sue6
2 | Bob6
5 | Sue7
3 | Bob7
6 | Sue8 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 48 | Bob2/Bob = 13/48 = 0.2708(3)
6 | Sue1 | Win
1 | Sue1
4 | Bob1
5 | Sue2
4 | Bob2
2 | Sue3
5 | Bob3
6 | Sue4 | Win
3 | Sue1
2 | Bob1
1 | Sue2
2 | Bob2
5 | Sue3
2 | Bob3
6 | Sue4 | Win
3 | Sue1
3 | Bob1
2 | Sue2
3 | Bob2
2 | Sue3
2 | Bob3
3 | Sue4
1 | Bob4
6 | Sue5 | Win
6 | Sue1 | Win
2 | Sue1
4 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 49 | Recording Bob2: 14 | Bob2/Bob = 14/49 = 2/7 = 0.(285714)
6 | Sue1 | Win
4 | Sue1
1 | Bob1
4 | Sue2
2 | Bob2
1 | Sue3
2 | Bob3
3 | Sue4
1 | Bob4
4 | Sue5
2 | Bob5
1 | Sue6
3 | Bob6
4 | Sue7
2 | Bob7
6 | Sue8 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 50 | Bob2/Bob = 14/50 = 7/25 = 0.28
5 | Sue1
5 | Bob1
1 | Sue2
5 | Bob2
5 | Sue3
4 | Bob3
1 | Sue4
4 | Bob4
1 | Sue5
2 | Bob5
2 | Sue6
5 | Bob6
1 | Sue7
3 | Bob7
6 | Sue8 | Win
3 | Sue1
2 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 51 | Recording Bob2: 15 | Bob2/Bob = 15/51 = 5/17 = 0.(2941176470588235)
6 | Sue1 | Win
4 | Sue1
4 | Bob1
6 | Sue2 | Win
1 | Sue1
6 | Bob1 | Win | Recording Bob: 52 | Bob2/Bob = 15/52 = 0.28(846153)
2 | Sue1
6 | Bob1 | Win | Recording Bob: 53 | Bob2/Bob = 15/53 = 0.(2830188679245)
5 | Sue1
4 | Bob1
2 | Sue2
5 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 54 | Bob2/Bob = 15/54 = 5/18 = 0.2(7)
3 | Sue1
4 | Bob1
1 | Sue2
4 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 55 | Bob2/Bob = 15/55 = 3/11 = 0.(27)
2 | Sue1
2 | Bob1
4 | Sue2
2 | Bob2
3 | Sue3
4 | Bob3
2 | Sue4
2 | Bob4
5 | Sue5
2 | Bob5
1 | Sue6
3 | Bob6
3 | Sue7
5 | Bob7
4 | Sue8
3 | Bob8
3 | Sue9
4 | Bob9
2 | Sue10
6 | Bob10 | Win | Recording Bob: 56 | Bob2/Bob = 15/56 = 0.267(857142)
6 | Sue1 | Win
6 | Sue1 | Win
3 | Sue1
5 | Bob1
3 | Sue2
4 | Bob2
6 | Sue3 | Win
6 | Sue1 | Win
1 | Sue1
5 | Bob1
6 | Sue2 | Win
3 | Sue1
6 | Bob1 | Win | Recording Bob: 57 | Bob2/Bob = 15/57 = 5/19 = 0.(263157894736842105)
3 | Sue1
2 | Bob1
6 | Sue2 | Win
2 | Sue1
6 | Bob1 | Win | Recording Bob: 58 | Bob2/Bob = 15/58 = 0.2(5862068965517241379310344827)
5 | Sue1
1 | Bob1
6 | Sue2 | Win
6 | Sue1 | Win
5 | Sue1
5 | Bob1
1 | Sue2
1 | Bob2
3 | Sue3
4 | Bob3
6 | Sue4 | Win
4 | Sue1
2 | Bob1
6 | Sue2 | Win
5 | Sue1
3 | Bob1
4 | Sue2
1 | Bob2
6 | Sue3 | Win
3 | Sue1
3 | Bob1
3 | Sue2
5 | Bob2
3 | Sue3
4 | Bob3
4 | Sue4
3 | Bob4
6 | Sue5 | Win
5 | Sue1
3 | Bob1
5 | Sue2
4 | Bob2
2 | Sue3
6 | Bob3 | Win | Recording Bob: 59 | Bob2/Bob = 15/59 = 0.(2542372881355932203389830508474576271186440677966101694915)
4 | Sue1
6 | Bob1 | Win | Recording Bob: 60 | Bob2/Bob = 15/60 = 1/4 = 0.25
3 | Sue1
2 | Bob1
2 | Sue2
2 | Bob2
2 | Sue3
2 | Bob3
4 | Sue4
6 | Bob4 | Win | Recording Bob: 61 | Bob2/Bob = 15/61 = 0.(245901639344262295081967213114754098360655737704918032786885)
1 | Sue1
1 | Bob1
6 | Sue2 | Win
5 | Sue1
5 | Bob1
1 | Sue2
6 | Bob2 | Win | Recording Bob: 62 | Recording Bob2: 16 | Bob2/Bob = 16/62 = 8/31 = 0.(258064516129032)
4 | Sue1
6 | Bob1 | Win | Recording Bob: 63 | Bob2/Bob = 16/63 = 0.(253968)
1 | Sue1
1 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 64 | Recording Bob2: 17 | Bob2/Bob = 17/64 = 0.265625
5 | Sue1
1 | Bob1
6 | Sue2 | Win
4 | Sue1
2 | Bob1
4 | Sue2
1 | Bob2
1 | Sue3
5 | Bob3
4 | Sue4
5 | Bob4
2 | Sue5
4 | Bob5
4 | Sue6
3 | Bob6
1 | Sue7
6 | Bob7 | Win | Recording Bob: 65 | Bob2/Bob = 17/65 = 0.2(615384)
3 | Sue1
2 | Bob1
2 | Sue2
2 | Bob2
5 | Sue3
1 | Bob3
3 | Sue4
4 | Bob4
3 | Sue5
3 | Bob5
1 | Sue6
3 | Bob6
2 | Sue7
5 | Bob7
6 | Sue8 | Win
3 | Sue1
3 | Bob1
1 | Sue2
1 | Bob2
4 | Sue3
6 | Bob3 | Win | Recording Bob: 66 | Bob2/Bob = 17/66 = 0.2(57)
4 | Sue1
6 | Bob1 | Win | Recording Bob: 67 | Bob2/Bob = 17/67 = 0.(253731343283582089552238805970149)
2 | Sue1
4 | Bob1
3 | Sue2
6 | Bob2 | Win | Recording Bob: 68 | Recording Bob2: 18 | Bob2/Bob = 18/68 = 9/34 = 0.2(6470588235294117)
1 | Sue1
6 | Bob1 | Win | Recording Bob: 69 | Bob2/Bob = 18/69 = 6/23 = 0.(2608695652173913043478)
3 | Sue1
5 | Bob1
1 | Sue2
2 | Bob2
3 | Sue3
3 | Bob3
5 | Sue4
3 | Bob4
2 | Sue5
3 | Bob5
5 | Sue6
2 | Bob6
5 | Sue7
1 | Bob7
5 | Sue8
3 | Bob8
2 | Sue9
1 | Bob9
4 | Sue10
4 | Bob10
3 | Sue11
1 | Bob11
2 | Sue12
1 | Bob12
4 | Sue13
1 | Bob13
2 | Sue14
2 | Bob14
4 | Sue15
6 | Bob15 | Win | Recording Bob: 70 | Bob2/Bob = 18/70 = 9/35 = 0.2(571428)
1 | Sue1
4 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 71 | Recording Bob2: 19 | Bob2/Bob = 19/71 = 0.(26760563380281690140845070422535211)
5 | Sue1
6 | Bob1 | Win | Recording Bob: 72 | Bob2/Bob = 19/72 = 0.263(8)
3 | Sue1
6 | Bob1 | Win | Recording Bob: 73 | Bob2/Bob = 19/73 = 0.(26027397)
3 | Sue1
3 | Bob1
1 | Sue2
3 | Bob2
2 | Sue3
5 | Bob3
3 | Sue4
4 | Bob4
4 | Sue5
5 | Bob5
4 | Sue6
6 | Bob6 | Win | Recording Bob: 74 | Bob2/Bob = 19/74 = 0.2(567)
4 | Sue1
1 | Bob1
4 | Sue2
4 | Bob2
1 | Sue3
5 | Bob3
5 | Sue4
5 | Bob4
6 | Sue5 | Win
6 | Sue1 | Win
2 | Sue1
2 | Bob1
5 | Sue2
4 | Bob2
3 | Sue3
3 | Bob3
5 | Sue4
3 | Bob4
5 | Sue5
5 | Bob5
5 | Sue6
3 | Bob6
4 | Sue7
2 | Bob7
3 | Sue8
6 | Bob8 | Win | Recording Bob: 75 | Bob2/Bob = 19/75 = 0.25(3)
5 | Sue1
5 | Bob1
2 | Sue2
2 | Bob2
4 | Sue3
5 | Bob3
3 | Sue4
2 | Bob4
2 | Sue5
5 | Bob5
3 | Sue6
4 | Bob6
6 | Sue7 | Win
2 | Sue1
4 | Bob1
6 | Sue2 | Win
2 | Sue1
4 | Bob1
6 | Sue2 | Win
5 | Sue1
2 | Bob1
5 | Sue2
1 | Bob2
1 | Sue3
4 | Bob3
3 | Sue4
5 | Bob4
3 | Sue5
3 | Bob5
1 | Sue6
4 | Bob6
5 | Sue7
6 | Bob7 | Win | Recording Bob: 76 | Bob2/Bob = 19/76 = 1/4 = 0.25
4 | Sue1
3 | Bob1
2 | Sue2
1 | Bob2
2 | Sue3
5 | Bob3
3 | Sue4
4 | Bob4
6 | Sue5 | Win
5 | Sue1
1 | Bob1
1 | Sue2
5 | Bob2
6 | Sue3 | Win
4 | Sue1
5 | Bob1
5 | Sue2
1 | Bob2
1 | Sue3
4 | Bob3
1 | Sue4
6 | Bob4 | Win | Recording Bob: 77 | Bob2/Bob = 19/77 = 0.(246753)
5 | Sue1
1 | Bob1
5 | Sue2
3 | Bob2
5 | Sue3
6 | Bob3 | Win | Recording Bob: 78 | Bob2/Bob = 19/78 = 0.2(435897)
6 | Sue1 | Win
5 | Sue1
6 | Bob1 | Win | Recording Bob: 79 | Bob2/Bob = 19/79 = 0.(2405063291139)
6 | Sue1 | Win
2 | Sue1
5 | Bob1
5 | Sue2
6 | Bob2 | Win | Recording Bob: 80 | Recording Bob2: 20 | Bob2/Bob = 20/80 = 1/4 = 0.25
4 | Sue1
6 | Bob1 | Win | Recording Bob: 81 | Bob2/Bob = 20/81 = 0.(246913580)
5 | Sue1
1 | Bob1
6 | Sue2 | Win
5 | Sue1
3 | Bob1
1 | Sue2
5 | Bob2
3 | Sue3
6 | Bob3 | Win | Recording Bob: 82 | Bob2/Bob = 20/82 = 10/41 = 0.(24390)
3 | Sue1
5 | Bob1
4 | Sue2
4 | Bob2
5 | Sue3
2 | Bob3
1 | Sue4
1 | Bob4
2 | Sue5
1 | Bob5
6 | Sue6 | Win
6 | Sue1 | Win
4 | Sue1
1 | Bob1
2 | Sue2
1 | Bob2
2 | Sue3
4 | Bob3
4 | Sue4
4 | Bob4
1 | Sue5
2 | Bob5
5 | Sue6
2 | Bob6
2 | Sue7
5 | Bob7
5 | Sue8
1 | Bob8
6 | Sue9 | Win
1 | Sue1
5 | Bob1
2 | Sue2
3 | Bob2
6 | Sue3 | Win
3 | Sue1
5 | Bob1
5 | Sue2
1 | Bob2
4 | Sue3
5 | Bob3
2 | Sue4
4 | Bob4
3 | Sue5
4 | Bob5
3 | Sue6
Final Bob2/Bob = 20/82 = 10/41 = 0.(24390)
ˌɑrməˈɡɛˌtrɑn
It's worth reading through the comments on the original linkrumpole wrote:I obviously cannot understand the question even when jonathan tried to explain it.
My favourite explaination of the question was this one
The trouble for me was that once I fully understood the question it became clear I didn't have the maths skills to get to the solution.Another restatement of the problem for those who don’t get it:
“Bob and Sue played exactly one game with a fair in a closed room (but with a video camera to verify the result). They come out and report that Bob won the game (he rolled a 6 before Sue). Now Alice (who did not see the game) pipes up: “I will bet $10 against your $50 that won it on his 2nd turn! Any takers?” (This means if Bob won on his 2nd turn, then you pays $40, otherwise she pays you $10).
Please assume that there is no cheating, and Alice has no information that you do not have.
Is it a good bet to take? At exactly what payout is it an even bet?
If you believe the probability is 1/6 or 5/36 or 125/1296, you will think this is a good bet, because although you wager 5 times as much, you are at least 5 times as likely to win. If the probability is 1/6, then you win 5 times out of 6, while Alice wins 1 time out of 6, so 10:50 is an even bet. If the odds are 125/1296, they you are more than 9 times as likely to win as Alice, but you are wagering only 5 times as much!
Alice must have miscalculated! What a rube! Take the bet!
Alice, however, has calculated the probability as 275/1296, approximately 21%. Alice thus that you are slightly less than 4 times as likely to win (you win about 79% of the time, and Alice wins about 21% of the time), but you would be risking 5 times as much money.
Alice is trolling for suckers! Are you going to bite?
So, with money on the line, what is the true probability?
Hint: If you want to take the bet at $10 to $50, I will be happy to oblige you!
- Lackadaisical
- Shutout Match Winner
- Posts: 823
- Joined: Sun Dec 21, 2003 4:58 pm
- Location: Amsterdam, Netherlands
- Contact:
I suppose this is overkill, but it is said pictures say OVER 9000 words
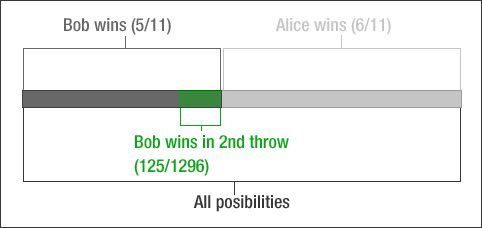
question: how much of the dark grey part is striped green

question: how much of the dark grey part is striped green
Official Officiant of the Official Armagetron Clan Registration Office
Back (in the sig) by popular demand: Lack draws
Back (in the sig) by popular demand: Lack draws
-
writingsama
- Posts: 1
- Joined: Fri Apr 03, 2009 8:42 am
Re: Nice puzzle
I had to register her just to post this. Sigh.
You're all wrong, because the puzzle is flawed, or intentionally much more deceptive than anyone anywhere seems to get.
Even the people who head down the clever, but incorrect road to arrive at 21.21% haven't taken into account the fact that there are an infinite number of cases in which neither one ever, ever rolls a 6, for all of eternity. Nowhere in the rules was it stated that eventually someone HAS to roll a 6 in general play and end the game. It didn't even state that the 6-sided die had a side denoting '6', nor did it state if it could move through an infinite number of iterations before one finally rolls a 6, but that's just getting into set theory pedantry that's unnecessary. Games can be infinite and never resolve, or infinite AND resolve, and you didn't search "all possible games" since you didn't search infinity. Except that in this SPECIFIC instance, it was stated that Bob *DID* eventually roll a 6. Sue did not, her odds of ever doing so are 0 over the whole of the game space, and his are 1, even over an infinitely large game space. The odds that it was on his second roll are uncomputable because of this basic fact: we don't know how long the game was. The odds are either 0 or 1, but we don't know. This problem is not possible to solve. You could say the odds it happened on the 2nd roll are infinitely small, I suppose. I.e. 0. This presents a paradox, since the puzzle explicitly stated that he did in fact roll a 6, eventually. This means the puzzle is actually a paradox with no resolution.
Or is it? Let’s look at it another way. The only question we *can* answer is what is the probability that he rolled *a* 6 on his second turn. That probability is 1/6. This is equivalent to asking *the* 6, because it is game-ending; in an infinite number of games which Sue does not roll a 6 before him, in which he does eventually roll a 6 and the game terminates, he will roll a 6 on his second turn with a probability of 1/6. No more rolls are made, and the sequence is made non-infinite, and thus computable. Thus, the probability that he rolled *the* 6 on his second roll is 1/6, because that’s the probability he will roll *a* 6 on *any* roll. This is seriously basic computability and probability, messed up by attempts to be clever that just aren’t clever enough, because of the deceptive nature of the puzzle. Sorry guys.
You're all wrong, because the puzzle is flawed, or intentionally much more deceptive than anyone anywhere seems to get.
Even the people who head down the clever, but incorrect road to arrive at 21.21% haven't taken into account the fact that there are an infinite number of cases in which neither one ever, ever rolls a 6, for all of eternity. Nowhere in the rules was it stated that eventually someone HAS to roll a 6 in general play and end the game. It didn't even state that the 6-sided die had a side denoting '6', nor did it state if it could move through an infinite number of iterations before one finally rolls a 6, but that's just getting into set theory pedantry that's unnecessary. Games can be infinite and never resolve, or infinite AND resolve, and you didn't search "all possible games" since you didn't search infinity. Except that in this SPECIFIC instance, it was stated that Bob *DID* eventually roll a 6. Sue did not, her odds of ever doing so are 0 over the whole of the game space, and his are 1, even over an infinitely large game space. The odds that it was on his second roll are uncomputable because of this basic fact: we don't know how long the game was. The odds are either 0 or 1, but we don't know. This problem is not possible to solve. You could say the odds it happened on the 2nd roll are infinitely small, I suppose. I.e. 0. This presents a paradox, since the puzzle explicitly stated that he did in fact roll a 6, eventually. This means the puzzle is actually a paradox with no resolution.
Or is it? Let’s look at it another way. The only question we *can* answer is what is the probability that he rolled *a* 6 on his second turn. That probability is 1/6. This is equivalent to asking *the* 6, because it is game-ending; in an infinite number of games which Sue does not roll a 6 before him, in which he does eventually roll a 6 and the game terminates, he will roll a 6 on his second turn with a probability of 1/6. No more rolls are made, and the sequence is made non-infinite, and thus computable. Thus, the probability that he rolled *the* 6 on his second roll is 1/6, because that’s the probability he will roll *a* 6 on *any* roll. This is seriously basic computability and probability, messed up by attempts to be clever that just aren’t clever enough, because of the deceptive nature of the puzzle. Sorry guys.
- Lackadaisical
- Shutout Match Winner
- Posts: 823
- Joined: Sun Dec 21, 2003 4:58 pm
- Location: Amsterdam, Netherlands
- Contact:
Re: Nice puzzle
But isn't the sum of all odds that the game lasts infinitively:
lim n-> ∞ (5/6)^n = 0
I'm not much of a mathematician, but I don't think having an infinite large game space necessarily means there is also an infinitely large probability space.
Total prob = 1/6 * sum(n=0 -> ∞) (5/6)^n = 1/6 * 1/(1-5/6) = 1
lim n-> ∞ (5/6)^n = 0
I'm not much of a mathematician, but I don't think having an infinite large game space necessarily means there is also an infinitely large probability space.
Total prob = 1/6 * sum(n=0 -> ∞) (5/6)^n = 1/6 * 1/(1-5/6) = 1
Official Officiant of the Official Armagetron Clan Registration Office
Back (in the sig) by popular demand: Lack draws
Back (in the sig) by popular demand: Lack draws
Re: Nice puzzle
Yes. It's possible that the game lasts forever, but infinitely improbable. It's a NULL-event that has no influence on the answer.Lackadaisical wrote:But isn't the sum of all odds that the game lasts infinitively:
lim n-> ∞ (5/6)^n = 0
writingsama: Just... no. You are right that the question needs interpretation, but wrong claiming our interpretation does not make sense. It is perfectly possible to work with experiments that possibly last forever, and it's perfectly possible to calculate probabilities of a) bob winning b) sue winning c) the game lasting forever d) bob winning on his second throw e) combining a) and b) to get the answer.
Re: Nice puzzle
I have never seen dice that look like this:

If we are talking about dice I think everyone thinks of a cube that has the numbers 1, 2, 3, 4 , 5 and 6 on its side. If it isn't a normal die although it belongs to the puzzle it should be part of the given information.
You can solve an exercise like "1+1=2" but this is more like "1+?=?..., oh and the + stands for - "!
alea iacta est.

If we are talking about dice I think everyone thinks of a cube that has the numbers 1, 2, 3, 4 , 5 and 6 on its side. If it isn't a normal die although it belongs to the puzzle it should be part of the given information.
You can solve an exercise like "1+1=2" but this is more like "1+?=?..., oh and the + stands for - "!
alea iacta est.
- Jonathan
- A Brave Victim
- Posts: 3391
- Joined: Thu Feb 03, 2005 12:50 am
- Location: Not really lurking anymore
Re: Nice puzzle
Convergence wins. See it like this. On the first roll, there's a 1/6 prob of winning, 5/6 of continuing. You can visualize that 5/6 as containing the next roll, which in turn contains the third and so on. Note how it never grows out of the original space. Now you can add all the 1/6 parts you like (as seen in the 'global' space), and get arbitrarily close to 1. That puts strong bounds on the influence of later turns. Even if you don't see how we did take it into account, you should get this.
ˌɑrməˈɡɛˌtrɑn